暗算を脳トレに取り入れてからしばらく経ちます。
特にふた桁✕ふた桁の暗算が好きで、暗算のやり方もいろいろ調べていました。
そうしたら、インド式計算ってなんかとても魅力的なのが出てきます。
インドと計算が結びついているところでもう調べずにはいられない感じ。
というわけで、さっそく本屋に行き、検索機でインド式と検索をかけると、ありました。
すぐに買いたかったんで今在庫があるやつをチョイス。
一冊で頭がよくなるインド式かんたん計算法という本を買ってきました。
一冊で頭がよくなるって表紙にかいてありますもん、もう脳トレどころの話じゃない!
もうワクワクで家に帰り見てみました。
インド式計算法
第一印象
計算法というと、どんな計算でも使える普遍的な方法なのかなと思っていましたが、こういう計算の時ははこうするというのがいっぱい書いてある、ひとつ覚えればそれですべてOK、って感じではないなというのが第一印象。
例えば2けたどうしの掛け算でいうと、11から19までの数字どうしの掛け算はこうする、十の位は等しく一の位を足すと10になる数字どうしの掛け算はこうするって感じです。
だから計算する時はこれはこのパターンでいけばいいとかをまず判断して計算を始める感じになると思います。
この時点でなんか、めんどくさ、ってなりますが、本、買っちゃったからね。
それに脳トレですから。パズルの一種ということで。。。
試しにやってみた
試しに11から19までどうしの掛け算をやってみました。
心の声と一緒に。。
14✕17
14+7=21(前の数字と2つ目の数字のひと桁目をなんで足すの?)
この時点で混乱の極みです。
4✕7=28(ひとけた目どうしで掛け算だからまあなんとなくいいか)
21✕10+28=238(ん?これで正解?)
機械的にこうすればいいって覚えてOKだといいんですが、もう意味が分からなくて心の中はモヤモヤだらけになってしまいました。
この本ではなんで?の答えも書いています。
11から19までの2つの数を
10+a,10+b
と置く
(10+a)✕(10+b)
=10×10+10b+10a+ab
=10x(10+a+b)+ab
そうなんだろうけどもっと実感としてわかりたいなと思いました。
中高でもっと勉強しとけばよかったんかな。
図のほうがイメージしやすいかも。
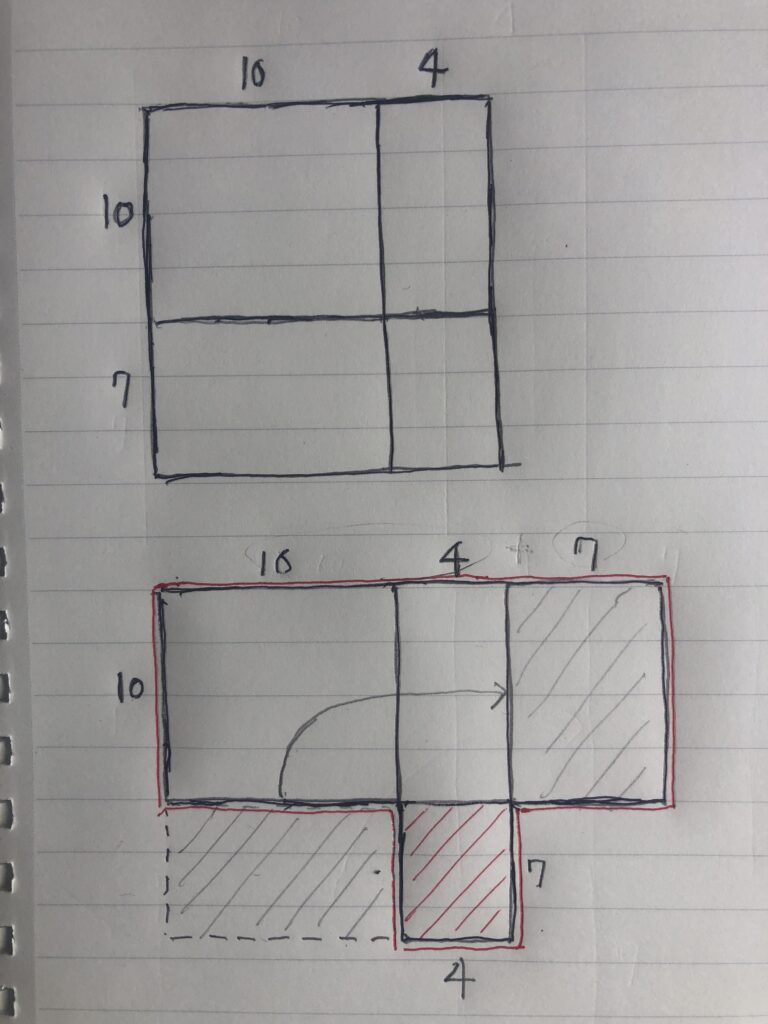
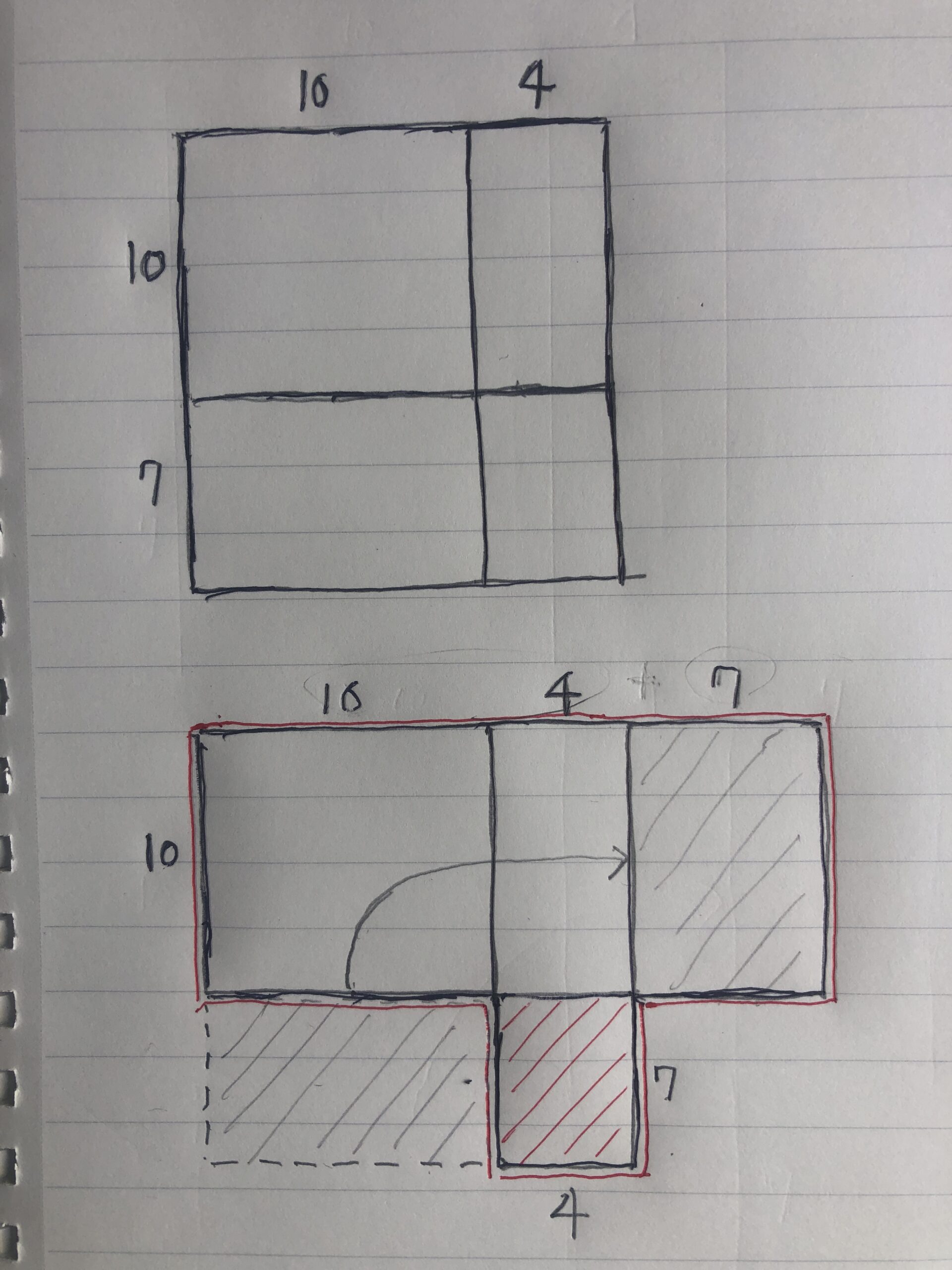
14✕17って上の図の四角です。
下の図は左下の斜線の四角を右上へ移動。
上の図を変形させた図で、赤で囲ったのが14✕17
赤の斜線は一の位どうしを掛けた部分です。
(14+7)✕10+(7✕4)
これでスッキリしました。
この本は図で解説してないので自分にとっては少しわかりにくかったですが、自分で図を書いた分やった感はありました。
結論、これはおもしろい
インド式計算法は、自分にとっては、なんで?から始まり、あーなるほど!で終わる。
そんな計算法です。
単純にやり方を丸暗記するだけだとこんなもんか、って感じですが、最初のなんで?を納得すると本質的な部分がイメージでわかり、楽しくなってきます。
計算も速くなると思います。
本質を理解し、やり方を柔軟に考えるというのは他のことにも通用することなんじゃないないかとか考えました。
まだ、掛け算をちょっとやっただけのインド式計算ですが、脳トレにももちろんなるし、何より面白いので、続けてやってみようと思いました。